Dynamic vibration control of non-linear buildings using multiple tuned mass dampers

Hashim  Ataie; Taiki  Saito

doi:10.59400/be.v1i1.488

Dynamic vibration control of non-linear buildings using multiple tuned mass dampers

Hashim Ataie Graduate School of Engineering, Toyohashi University of Technology, Toyohashi 441-8580, Japan
Taiki Saito Department of Architecture and Civil Engineering, Toyohashi University of Technology, Toyohashi 441-8580, Japan

Ariticle ID: 488

147 Views, 76 PDF Downloads

DOI: https://doi.org/10.59400/be.v1i1.488

Keywords: dynamic vibration control; multiple tuned mass dampers; non-linear building; control strategy; pushover capacity curve; modal effective mass

Abstract

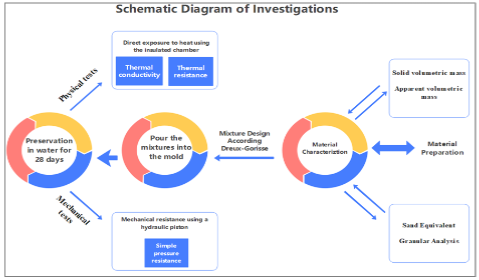
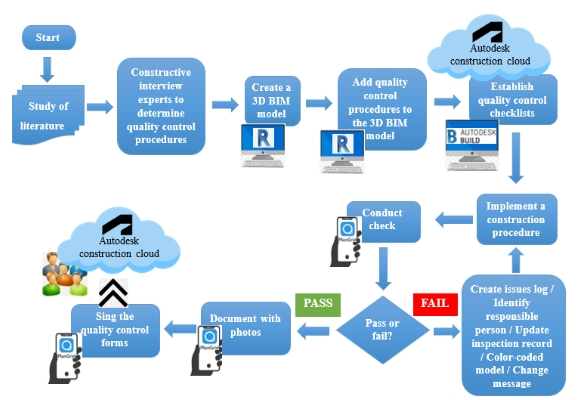
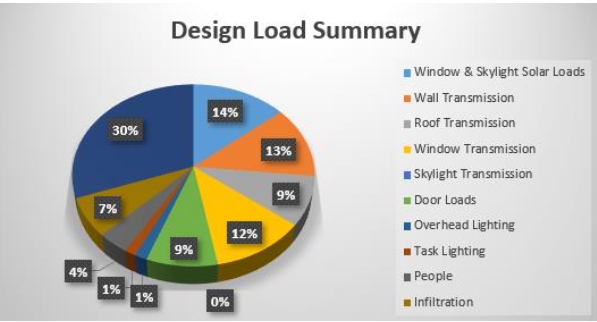
In the field of civil engineering, tuned mass dampers (TMDs) serve as passive devices designed for dynamic vibration control of structures. When dealing with buildings exhibiting nonlinear behavior under dynamic loads, the effectiveness of TMDs may be affected by detuning due to the degradation of the building’s strength. Therefore, addressing the non-linear behavior requires a unique strategy involving the tuning of TMDs to specific time periods following the onset of non-linearity. The proposed approach in this study entails a pushover analysis to establish the pushover capacity curve. The regions between the origin and a target drift of 1/150 are then represented using an idealized trilinear form, with the initial segment corresponding to linearity and subsequent segments capturing non-linear behavior. The second segment spans from the onset of non-linearity to a target drift of 1/400, and the third segment covers the drift range from 1/400 to 1/150. Examining this strategy involves calculating time periods for each segment. Subsequently, three single TMD (STMD) scenarios and one multiple TMD (MTMD) scenario with 3 TMDs, each tuned to time periods corresponding to specific segments of the idealized trilinear, are compared in this study. The evaluation includes non-linear dynamic analysis of 7-story and 25-story reinforced concrete buildings equipped with these TMD scenarios. The floor maximum displacement and peak acceleration results indicate that the STMDs tuned to the time periods corresponding to the non-linear segments exhibit robustness, surpassing the performance of the STMD tuned to the fundamental period. Remarkably, the MTMD scenario demonstrates superior robustness compared to all three STMD scenarios. Further analysis under wind load on the same 25-story building confirms the effectiveness of the MTMDs and STMD tuned to the nonlinearity segment compared to the STMD tuned to the fundamental period. This research provides valuable insights into TMD design for enhanced building performance under non-linear conditions.

References

[1] Boccamazzo A, Carboni B, Quaranta G, et al. Seismic effectiveness of hysteretic tuned mass dampers for inelastic structures. Engineering Structures 2020; 216: 110591. doi: 10.1016/j.engstruct.2020.110591

[2] Huang H, Mosalam KM, Chang WS. Adaptive tuned mass damper with shape memory alloy for seismic application. Engineering Structures 2020; 223: 111171. doi: 10.1016/j.engstruct.2020.111171

[3] Lu Z, Chen X, Zhang D, et al. Experimental and analytical study on the performance of particle tuned mass dampers under seismic excitation. Earthquake Engineering & Structural Dynamics 2016; 46(5): 697–714. doi: 10.1002/eqe.2826

[4] Elias S, Matsagar V. Seismic vulnerability of a non-linear building with distributed multiple tuned vibration absorbers. Structure and Infrastructure Engineering 2019; 15(8): 1103–1118. doi: 10.1080/15732479.2019.1602149

[5] Domizio M, Garrido H, Ambrosini D. Single and multiple TMD optimization to control seismic response of nonlinear structures. Engineering Structures 2022; 252: 113667. doi: 10.1016/j.engstruct.2021.113667

[6] Mohebbi M, Joghataie A. Designing optimal tuned mass dampers for nonlinear frames by distributed genetic algorithms. The Structural Design of Tall and Special Buildings 2011; 21(1): 57–76. doi: 10.1002/tal.702

[7] Shamsaddinlou A, Shirgir S, Hadidi A, et al. An efficient reliability-based design of TMD & MTMD in nonlinear structures under uncertainty. Structures 2023; 51: 258–274. doi: 10.1016/j.istruc.2023.03.053

[8] Sgobba S, Marano GC. Optimum design of linear tuned mass dampers for structures with nonlinear behaviour. Mechanical Systems and Signal Processing 2010; 24(6): 1739–1755. doi: 10.1016/j.ymssp.2010.01.009

[9] Roozbahan M, Jahani E. Optimal design of elastic and elastoplastic tuned mass dampers using the Mouth Brooding Fish algorithm for linear and nonlinear structures. Structures 2022; 43: 1084–1090. doi: 10.1016/j.istruc.2022.07.037

[10] Structural Earthquake Response Analysis Software, STERA-3D Version 11.4. Available online: http://www.rc.ace.tut.ac.jp/saito/software-e.html (accessed on 22 December 2023).

[11] Saito T. STERA-3D Technical Manual. Version 7.2. TUT; 2002.

[12] Tsai H, Lin G. Optimum tuned-mass dampers for minimizing steady-state response of support-excited and damped systems. Earthquake Engineering & Structural Dynamics 1993; 22(11): 957–973. doi: 10.1002/eqe.4290221104

[13] Conner JJ. Introduction to Structural Motion Control. Pearson Education, Inc; 2003. pp. 217–285.

[14] Global component of the center for engineering strong motion data. Strong-motion virtual data center. Available online: https://www.strongmotioncenter.org/vdc/scripts/search.plx (accessed on 22 December 2023).

[15] National center for environmental information. NOAA. Available online: https://www.ngdc.noaa.gov/hazel/view/hazards/earthquake/search (accessed on 22 December 2023).

[16] ViewWave Software Version 2.2.6. Kashima’s Office. Available online: https://smo.kenken.go.jp/~kashima/viewwave/download (accessed on 22 December 2023).

[17] NatHaz on-line wind simulator (NOWS). Available online: http://windsim.ce.nd.edu/gew_init2.html (accessed on 22 December 2023).

[18] Banerjee S, Ghosh AD, Matsagar VA. Optimum design of nonlinear tuned mass damper for dynamic response control under earthquake and wind excitation. Struct Control Heal Monit 2022; 29(7). doi: 10.1002/stc.2960

Published

2023-12-30

How to Cite

Ataie, H., & Saito, T. (2023). Dynamic vibration control of non-linear buildings using multiple tuned mass dampers. Building Engineering, 1(1), 488. https://doi.org/10.59400/be.v1i1.488

Download Citation

Issue

Vol. 1 No. 1 (2023)

Section

Article

This work is licensed under a Creative Commons Attribution 4.0 International License.

Editor-in-Chief

Prof. Scholz Miklas
University of Johannesburg, South Africa

eISSN

3029-2670

Publication Frequency

Semi-annual

About the Publisher

Academic Publishing insists on taking academic exchange and publication as the main line, carrying out comprehensive management based on science and technology, and fully exploring excellent international publishing resources. Within 5 years, it will form a strategic framework and scale with science (S), technology (T), medicine (M), education (E), and humanities and arts (H) as the main publishing fields. Academic Publishing is headquartered in Singapore and based in Malaysia, with the United States and China providing the main scientific and academic resources. At the same time, it has established long-term good cooperative relations with other publishing companies, scientific research communities, and academic organizations in more than a dozen countries and regions. Academic Publishing uses English and Chinese as its main publishing languages, mainly publishing books, journals, and conference papers in print and online. The vast majority of publications follow the international open access policy, providing stable and long-term quality and professional publications. With the joint efforts of the expert team and our professional editorial team, our publications will gradually be indexed by international databases in stages to provide convenient and professional retrieval for various scholars. At the same time, manuscripts we accept will be subject to the peer review principle, and cutting-edge and innovative research articles will be preferentially accepted for peer reference and discussion. All kinds of our publications are welcome for peer to contribute, access, and download.

more

Volume Arrangement

2024

Vol 2, No 2 (2024)

Vol 2, No 1 (2024)

2023

Vol 1, No 1 (2023)

Featured Articles

Comprehensive seismic loss model of Tehran, Iran in the case of Mosha fault seismic scenario using stochastic finite-fault method

This paper presents the results of a study caried out to assess probable seismic loss, in term of damage to the residential buildings and the number of fatalities, in the case of Mosha Fault seismic scenario in Tehran, Iran. Accordingly, seismic risk components (including seismic hazard, exposure model and fragility curves) are evaluated. The stochastic finite-fault method with dynamic corner frequency is applied for quantifying ground motion values. The results shows that PGA on the soil surface could range between 0.1 g to 0.45 g. Then, a reliable model of building exposure by analyzing census data from Tehran is compiled. This model included 19 different classes of buildings and is used to evaluate the potential damage to buildings from seismic scenario. The results indicate that the median of damage ratio from 100,000 iterations for the whole of the city is about 6% ± 1.54%. The study found that the central and eastern parts of Tehran are the most vulnerable areas, with an estimated 15,952 residents at risk of losing their lives in this scenario. This is equivalent to 0.2 percent of total population of Tehran. The finding from this study can be used by local authorities to provide appropriate emergency-response and preparedness plans in the case of Mosha Fault seismic scenario.

Digital transformation of quality management in the construction industry during the execution phase by integration of building information modeling (BIM) and cloud computing

The quality of construction projects significantly impacts social and economic development. However, low quality and project failure often result from factors such as lack of quality procedures, poor communication, task coordination, and inefficient progress monitoring. This research aims to improve the efficiency of the construction phase by creating quality control checklists for processes and enhancing quality management through a collaborative digital environment integrating building information modeling (BIM) and cloud computing. Expert constructive interviews were first conducted to define a construction process quality control procedure to be linked to the 3DBIM model and then transition to a collaborative cloud environment (Autodesk Construction Cloud). An actual instance in Latakia City (Syria) demonstrated that the proposed methodology improves the efficiency and effectiveness of quality management during the implementation phase. It does so by offering a robust database, enhancing on-site quality information extraction from BIM models using smartphones, documenting defects and entering inspection data directly into a shared digital environment, and making it easier to track corrective actions and feedback. This facilitates constant and organized access to current data, reducing errors and rework, saving money and time, and enhancing decision-making speed and effectiveness. The search recommends the necessity of strict laws to adhere to quality procedures and the importance of providing infrastructure for digital transformation in quality management.

Net zero energy analysis and energy conversion of sustainable residential building in Muscat, Oman

The building sector is the predominant consumer of primary energy globally. The building sector accounts for around 40% of global energy production.Net Zero Energy Buildings (NZEBs) are highly suggested by energy experts as an effective option to alleviate the strain on primary energy sources caused by the building sector. The disparity between energy performance predictions provided during the design phase and the actual energy performance of residential buildings is mostly attributed to a limited comprehension of the components that influence energy consumption and the constraints of whole building simulation software. The objective of this research was to perform a comparison analysis of the expected and actual energy consumption of a prototype net-zero energy house built at the University of Technology and Applied Sciences in Muscat. The Hourly Analysis Programme (HAP V4.2) was utilised to forecast the energy consumption of a Net Zero Energy Building (NZEB) at HCT, taking into account the availability of an Energy Recovery Ventilator (ERV) and the absence of an ERV. The newly built house underwent a one-month testing phase to fulfil many duties according to competition regulations. One of the main goals was to generate on-site energy through photovoltaic panels, producing an amount proportional to the energy consumed by the house. Upon comparing the actual energy consumption data with the simulated result, it was noticed that the actual energy demand of the house was around 20% lower than the prediction made by the simulation tool.

Architecting sustainability performances and enablers for grid-interactive efficient buildings

Today, grid-interactive efficient buildings are gaining popularity due to their potential sustainability performances through their ability to learn, adapt, and evolve at different scales to improve the quality of life of their users while optimizing resource usage and service availability. This is realized through various practices such as management and control measures enabled by smart grid technologies, interoperability, and human-cyber-physical security. However, despite their great potential, the research of those technologies still faces various challenges. These include a lack of communication and control infrastructure to address interpretability, security, cost barriers, and difficulties balancing occupant needs with grid benefits. Initially, system modelling and simulation are promising approaches to address those challenges ahead of time. It involves the consideration of complex systems made up of components from various research domains. This paper addresses the above practices, highlighting the value of integrating technology and intelligence in the planning and operation of buildings, both new and old. It provides a way to educate architects and engineers about this emerging field and demonstrates how these practices can help in creating efficient, resilient, and secure buildings that contribute to occupant comfort and decarbonization.