Gravitational redshift explained as a Doppler Effect in uniformly accelerated frames

A. Sfarti

doi:10.59400/jam.v1i2.156

Gravitational redshift explained as a Doppler Effect in uniformly accelerated frames

A. Sfarti CS Department, 387 Soda Hall, UC Berkeley, Berkeley, CA 94720, USA

Ariticle ID: 156

45 Views, 7 PDF Downloads

DOI: https://doi.org/10.59400/jam.v1i2.156

Keywords: Pound-Rebka, Gravitational Redshift, Tests of General Relativity, Einstein Equivalence Principle, Doppler Effect for uniformly accelerated motion, Error Analysis for Numerical Methods

Abstract

Einstein predicted a change in the energy of photons in the proximity of a gravitational field, the change being directly proportional with the distance from the gravitational source. In the early 60’s Pound and Rebka have set to verify Einstein’s prediction. The experiment was reprised with even higher precision by Pound and Snider. Later, Vessot reprised the experiment in space at a much improved precision. The standard explanation of gravitational redshift falls out straight from the Schwarzschild solution of the Einstein Field Equations (EFE). In the following, we will present an approach to the experiment relying on the Einstein Equivalence Principle and on the recently derived expressions of Doppler Effect for uniformly accelerated motion of the source and the receiver. We will conclude with a chapter on the numerical limits of applicability of the described method.

References

Pound RV, Rebka GA Jr. Resonant absorption of the 14.4-kev gamma Ray from 0.10-µsec Fe57. Physical Review Letters 1959; 3(12): 554. doi: 10.1103/PhysRevLett.3.554

Pound RV, Snider JL. Effect of gravity on nuclear resonance. Physical Review Letters 1964; 13(18): 539–540. doi: 10.1103/physrevlett.13.539

Vessot RFC, Levine MW, Mattison EM, et al. Test of relativistic gravitation with a space-borne hydrogen maser. Physical Review Letters 1980; 45(26): 2081–2084. doi: 10.1103/physrevlett.45.2081

Einstein A. On the electrodynamics of moving bodies. Annalen der Physik 1905; 17: 891–921.

Will CM. The confrontation between general relativity and experiment. Living Reviews in Relativity 2001; 4(1): 4. doi: 10.12942/lrr-2001-4

Vessot RFC, Levine MW. A test of the equivalence principle using a space-borne clock. General Relativity and Gravitation 1979; 10(3): 181–204. doi: 10.1007/bf00759854

Taylor JH. Astronomical and Space Experiments to Test Relativity. Cambridge University Press; 1987. pp. 209–222.

Feynman RP, Wagner WG, Morinigo FB, et al. Feynman Lectures on Gravitation. Addison-Wesley; 1995.

Misner CW, Thorne KS, Wheeler JA. Gravitation. W. H. Freeman and Company; 1973.

Desloge EA. Nonequivalence of a uniformly accelerating reference frame and a frame at rest in a uniform gravitational field. American Journal of Physics 1989; 57(12): 1121–1125. doi: 10.1119/1.15802

Desloge EA. The gravitational red shift in a uniform field. American Journal of Physics 1990; 58(9): 856–858. doi: 10.1119/1.16349

Dicke RH. New research on old gravitation. Science 1959; 129(3349): 621–624. doi: 10.1126/science.129.3349.621

Dicke RH. Mach’s principle and equivalence. In: Møller C (editor). Evidence for Gravitational Theories: Proceedings of Course 20 of the International School of Physics “Enrico Fermi”. Academic Press; 1962.

Einstein A. About the Principle of Relativity and the Conclusions Drawn from it (German). Jahrbuch der Radioaktivitaet und Elektronik; 1907.

Einstein A. On the influence of gravity on the propagation of light. Annalen der Physik 1911; 340(10): 898–908. doi: 10.1002/andp.19113401005

Brans CH. The roots of scalar-tensor theory: An approximate history. arXiv 2005; arXiv:gr-qc/0506063. doi: 10.48550/arXiv.gr-qc/0506063

Ohanian HC, Ruffini R. Gravitation and Spacetime, 2nd ed. W. W. Norton & Company; 1994.

Uzan JP. The fundamental constants and their variation: Observational and theoretical status. Reviews of Modern Physics 2003; 75(2): 403–455. doi: 10.1103/revmodphys.75.403

Will CM. Theory and Experiment in Gravitational Physics. Cambridge University Press; 1993.

Niebauer TM, Sasagawa GS, Faller JE, et al. A new generation of absolute gravimeters. Metrologia 1995; 32(3): 159–180. doi: 10.1088/0026-1394/32/3/004

Peters A, Chung KY, Chu S. High-precision gravity measurements using atom interferometry. Metrologia 2001; 38(1): 25–61. doi: 10.1088/0026-1394/38/1/4

Linet B, Teyssandier P. Time transfer and frequency shift to the order 1/c4 in the field of an axisymmetric rotating body. Physical Review D 2002; 66(2): 024045. doi: 10.1103/physrevd.66.024045

Sfarti A. QED-based derivation of the general forms of the relativistic Doppler effect and of the relativistic aberration for uniformly rotating frames and for uniformly accelerated frames. Modern Physics Letters A 2022; 37: 37n38. doi: 10.1142/s0217732322502388

Published

2023-08-18

How to Cite

Sfarti, A. (2023). Gravitational redshift explained as a Doppler Effect in uniformly accelerated frames. Journal of AppliedMath, 1(2), 156. https://doi.org/10.59400/jam.v1i2.156

Download Citation

Issue

Vol. 1 No. 2 (2023)

Section

Article

This work is licensed under a Creative Commons Attribution 4.0 International License.

Editor-in-Chief

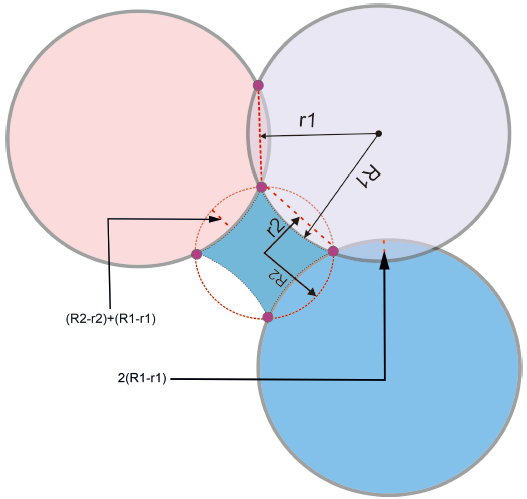
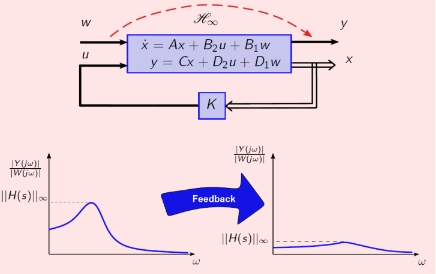
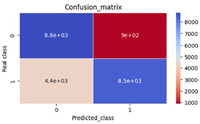
Assoc. Prof. Ahmad Zeeshan

International Islamic University Pakistan

eISSN

2972-4805 (O)

Publication Frequency

Bi-monthly

About the Publisher

Academic Publishing insists on taking academic exchange and publication as the main line, carrying out comprehensive management based on science and technology, and fully exploring excellent international publishing resources. Within 5 years, it will form a strategic framework and scale with science (S), technology (T), medicine (M), education (E), and humanities and arts (H) as the main publishing fields. Academic Publishing is headquartered in Singapore and based in Malaysia, with the United States and China providing the main scientific and academic resources. At the same time, it has established long-term good cooperative relations with other publishing companies, scientific research communities, and academic organizations in more than a dozen countries and regions. Academic Publishing uses English and Chinese as its main publishing languages, mainly publishing books, journals, and conference papers in print and online. The vast majority of publications follow the international open access policy, providing stable and long-term quality and professional publications. With the joint efforts of the expert team and our professional editorial team, our publications will gradually be indexed by international databases in stages to provide convenient and professional retrieval for various scholars. At the same time, manuscripts we accept will be subject to the peer review principle, and cutting-edge and innovative research articles will be preferentially accepted for peer reference and discussion. All kinds of our publications are welcome for peer to contribute, access, and download.

more

Volume Arrangement

2024

2023

Featured Articles

H∞ hybrid control and MRD in a steel frame building subjected to excessivevibrations caused by the dynamic action of wind and earthquake

The dynamic loads from earthquakes and winds can destroy lives, cause collapse in civil structures, and interrupt basic services provided to the population. In this scenario, structural designs must be developed to decrease the damage induced by these actions. The objective of this work is to design a hybrid controller based on the H∞ optimization via state feedback and the magneto-rheological damper (MRD) to mitigate the excessive vibrations of a three-story steel frame building, represented through the shear building model, subjected to the simultaneous dynamic action of wind and earthquake. All research is based on computational simulation, experimental research and results will not be addressed. In the numerical analysis, digital computer and MATLAB® software are used, and implemented codes generate the expected results based on the mathematical modeling. With the application of the H∞ control technique via state feedback, the displacements were reduced by 77%. With MRD this reduction was 79%. With the hybrid controller, this reduction was 100%. Thus, the verifications in relation to maximum displacements were met for NBR 15421:2006, NBR 8800:2008 and NBR 6118:2014. From the results, it is concluded that the hybrid controller proved to be more efficient and achieved the proposed objective. The exogenous inputs had zero influence on the behavior of the system output.

Topological analysis of multiple tables

The paper proposes a topological approach in order to explore several data tables simultaneously. These data tables of quantitative and/or qualitative variables measured on different homogeneous themes, collected from the same individuals. This approach, called topological analysis of multiple tables (TAMT), is based on the notion of neighborhood graphs in the context of a joint analysis of several data tables. It allows the simultaneous study of possible links between several thematic tables. The structure of the correlations or associations of the variables in each thematic table is analyzed according to quantitative, qualitative or mixed variables considered. Like the multiple factorial analysis (MFA), the TAMT allows several tables of variables to be analyzed simultaneously, and to obtain results, in particular graphical representations, which make it possible to study the relationship between individuals, variables and tables of data. These can also be tables of temporal data, collected at different times on the same individuals. The proposed TAMT approach is illustrated using real data associated with several and different homogeneous themes. Its results are compared to those from the MFA method.

Development of a stacked hybrid Decision Tree model leveraging the NSL-KDD dataset

Intrusion detection in information technology as well as operational technology networks is highly required in modern day systems due to the increased spate of cyber-attacks in both number and complexity. Anomaly-based intrusion detection systems which have the capacity to detect novel or zero-day attacks are highly employed in this regard. One important component of anomaly-based intrusion detection systems which ensures their behaviour is artificial intelligence in general and machine learning in particular. The burden in modern day cybersecurity research is to investigate and develop models that can outperform existing ones. This paper is aimed at developing a hybrid decision tree model using the stacking ensemble approach. Performances were measured on the basis of recall, precision, accuracy, F1-score, receiver operating characteristics and confusion matrices. The hybrid model presented a precision of 97%, accuracy of 81%, F1-score of 80% and AUC score of 0.96, respectively.

The synergistic effect of the multiple parameters of vibro-impact nonlinear energy sink

This article studies the dynamics and efficiency of a vibro-impact damper (single-sided vibro-impact nonlinear energy sink—SSVI NES) depending on the exciting force parameters. The damper is coupled with a linear oscillator—the primary structure. It is shown that the damper is quite effective in a wide range of the exciting force amplitude and in the range of its frequency, which are higher than the resonant frequency; damper efficiency in these regions is fairly stable. The dynamics of the vibro-impact system “primary structure—SSVI NES” is rich and complex, which, however, does not impair the damper efficiency. In complex oscillatory regimes, the damper makes bilateral impacts: it hits both an obstacle and directly against the primary structure, which actually turns a single-sided NES into a double‐sided one. The optimization procedure and the choice of optimal damper parameters play a very important role in damper design. Optimizing multiple damper parameters instead of three shows a synergistic effect and provides better results.

Optimization imposition upon drone gimbal control electronics

The goal of the manuscript is to design a relatively good control structure for the noise suppression of a drone’s camera gimbal action. The gimbal’s movement can be simplified as a rest-to-rest reorientation system that can achieve the boundary result of a dynamic system. Six different control architectures are proposed and evaluated based on their ability to control the trajectory of the dynamic-system position and speed, their running time, and their quadratic cost. The robustness of the control architecture to uncertainties in inertia and sensor noise is also analyzed. Monte Carlo figures are used to assess the performance of the six control systems. The conditions for applying different architectures are identified through this analysis. The analysis and experimental tests reveal the most suitable control of the drone’s camera gimbal rotation.